Teknoloji Haberleri
Aşağı Git
Tüm Forumlar
Eğitim ve Sınavlar
Üniversite Eğitimi ve Yüksek Lisans, Doktora
(Güncel)Karmaşık Sayılar..Sınav var.Yardım
Bu konudaki kullanıcılar: 1 misafir
31
Cevap 5093
Tıklama 0
Öne Çıkarma
Cevap 5093
Tıklama 0
Öne Çıkarma
-
(Güncel)Karmaşık Sayılar..Sınav var.Yardım
|
Karmaşık düzlemde z1 ve z2 karmaşık sayılarını yerleştirince z1 ile z2 arasında kalan açı 90 derece olur. Sayıların mutlak değerleri de 1 olduğu için hipotnüs kök2 olur. M(0,6)miş karmaşık düzlemde bu noktayı alıp çember çiz sonra bu çembere teğet 2 doğru çiz. Çemberin yarıçapını alınca orada dik üçgen oluşacak, 90ın karşısında 6 olduğuna göre yarıçapa bakan açı 30 derece olacak. En büyüğünü istediği için 2. teğete kadar olan açıyı baz alacağız 90+30dan en büyüğü 120 en küçüğü de ilk teğet baz alınacağı için 90-30dan 60 olacak |
Bu mesaja 1 cevap geldi.
Çok teşekkürler. |
çok teşekkür ederim 3.soruda yaptıgın dönüşümleri anlayamadım ama ya |
Ya helal olsun sana harbi anladım ya kaç gündür bunla uraşıyodum çok sagol  Burda yine yapamadıgım soruları paylaşırım ben yardımcı olursan sevinirim. |
Anlamadığın yer olursa sorarsın.
5. soru  |
çok iyisin ya  yeni sorularda var  |
6. soruda mesela z1 üssü 3 değilde 3.z1 oldugundada yani bizden 3.z1'i istediğindede aynı şeyimi yapıyoruz. diğerleri tamamdır saolasın. |
Bu mesaja 1 cevap geldi.
| Aynısını yapmıyorsun. Atıyorum 1+i karmaşık sayın olsun argmenti 45tir bu sayıyı 6 ile çarp 6+6i den yine argüment 45 çıkacak, o yüzden katsayı argümenti etkilemez |
Bu mesaja 1 cevap geldi.
saolasın.peki 3argz1+2argz2 nasıl olur ? |
tamamdır.  |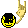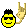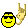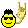
12.sorunun cevabının 10 çıkması lazım  11.soruda -2üssü10 diyoruz sonra 2üssü10cis180 oluyo ya o eksi nasıl artı oluyo ? 11.soru karışıkmış ya okurken beynim sulandı  |
tamamdır buldum  teşekkürler. 14. soruda işlem hatası yapıyorum galiba 30 kere denedim yanlış çıkıyo hep  |
< Bu mesaj bu kişi tarafından değiştirildi godilli -- 7 Kasım 2011; 0:48:14 >
| son soru -i çıkıyor yapacağın tek şey paydadaki ilerin eşleniklerini almak o kadar |
Bu mesaja 1 cevap geldi.
ya çıkmıyo ya çıkmıyo  |
16. sorunun cevabı -1miş.14.soruyu anlatırmısın bide ya |
eyvallah saolasın.15.soruya baktın mı ? |
17.soruda işlem hatası yapıyorum galiba cevap buluyorum ama yanlış çıkıyo . |
Z2=cos15+i.sin15 ise Z1-Z2 karmaşık sayısını bulun.
2)|z-6i|=3 koşulunu sağlayan z karmaşık sayılarından esas argümenti en küçük olanı ile en büyük olanının esas argümentlerini bulun.
3)sin70-i.cos70
-------------- = ?
-sin80+i.cos80
4)z=2.cis35 ve w=4.cis65 ise |z-w| kaçtır ?
5)(kök3-i)'nin 10. kuvveti kaçtır ?
6)argZ1=60 derece , argZ2=135 derece ise;
arg(Z1üssü3.Z2üssü2)=?
7)2-3i karmaşık sayısı orijin etrafında pozitif yönde 90 derece döndürülürse hangi karmaşık sayı elde edilir ?
8) iüssü2+iüssü3+iüssü4+.......+iüssü54+iüssü55 ifadesinin eşitini bulunuz.
9)1+a-bi
----------=z karmaşık sayısının başlangıç noktasına olan uzaklığını bulunuz.
b-ai-i
10) 1<|z-2|<eşit 2 eşitsizliğine karmaşık düzlemde karşılık gelen noktalar kümesini gösteriniz.
11)z=(1+i)üssü20 karmaşık sayısının kareköklerini bulunuz.
12)|z-2+i|<eşit 1 olmak üzere |z-6-2i| ifadesinin en küçük değeri ile en büyük değerinin toplamını bulunuz.
13)z=3-4i karmaşık sayısının kareköklerini bulunuz.
14)< Resime gitmek için tıklayın >
15)(a+bi)üssü20 ifadesinin açılımı yapıldıgında elde edilen terimlerin kat sayılar toplamı kaçtır ?
16)z=kökb-köka.i/köka+kökb.i ise Re(z)+Im(z) ifadesinin eşiti nedir ?
17)3z+4zi=i eşitliğini sağlayan z karmaşık sayısının başlangıç noktasına olan uzaklığı kaç birimdir ?
18)kök içinde 1+kök3i ifadesinin eşiti nedir ?
19)z=1-kök3i ise 1/zkare nin kutupsal biçimde ifadesi nedir ?
20)z=4-3i karmaşık sayısının esas argümenti alfa ise sin2alfa kaçtır ?
21)z=cos60/cos40+i.sin40 ise [Re(z)]kare + [Im(z)]kare ifadesinin eşiti nedir ?
22)Arg[z.(1-kök3i)]=320derece ise Arg(z) nedir ?
23)(1-cis60)üssü3=?
24)z1=cis200 ve z2=cis20 ise kökiçinde z1/z2 ifadesinin eşiti nedir ?
25)z1,z2,z3 karmaşık sayılarının esas argümentleri sırasıyla 120,15,108 ise z1üssü3.z2üssü4/z3üssü5 karmaşık sayısının esas argümenti nedir ?
26)0<alfa-beta<90derece olmak üzere z1=cosalfa+isinalfa ve z2=2(cosbeta+i.sinbeta) karmaşık sayıları arasındaki uzaklık kök3 ise z1.z2üssü-1 nedir ?
27)z karmaşık sayısı için argzüssü3+arg3/z=45derece ise arg(z) nedir ?
28)z=1-i/1-kök3i karmaşık sayısı için züssü6 ne olur?
çözebilecek olan ?
Edit= 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14 15. 16. sorular çözülmüştür.
DH forumlarında vakit geçirmekten keyif alıyor gibisin ancak giriş yapmadığını görüyoruz.
Üye Ol Şimdi DeğilÜye olduğunda özel mesaj gönderebilir, beğendiğin konuları favorilerine ekleyip takibe alabilir ve daha önce gezdiğin konulara hızlıca erişebilirsin.
< Bu mesaj bu kişi tarafından değiştirildi godilli -- 9 Kasım 2011; 22:50:49 >